Camera#

If a mutable has an attribute type of camera, it’s a camera. Typically, a simple pinhole camera model is used.

Required attributes of a camera:

Name	Type
camera_parameters	dict

camera_parameters is a dictionary with the following six required keys:

Name	Type
screen_width	int
screen_height	int
focal_length	numeric
horizontal_aperture	numeric
near_clip	numeric
far_clip	numeric

Pinhole Model#

3D objects are projected onto a 2D plane, like this:

Looking from a top view, towards the negative Y-axis:

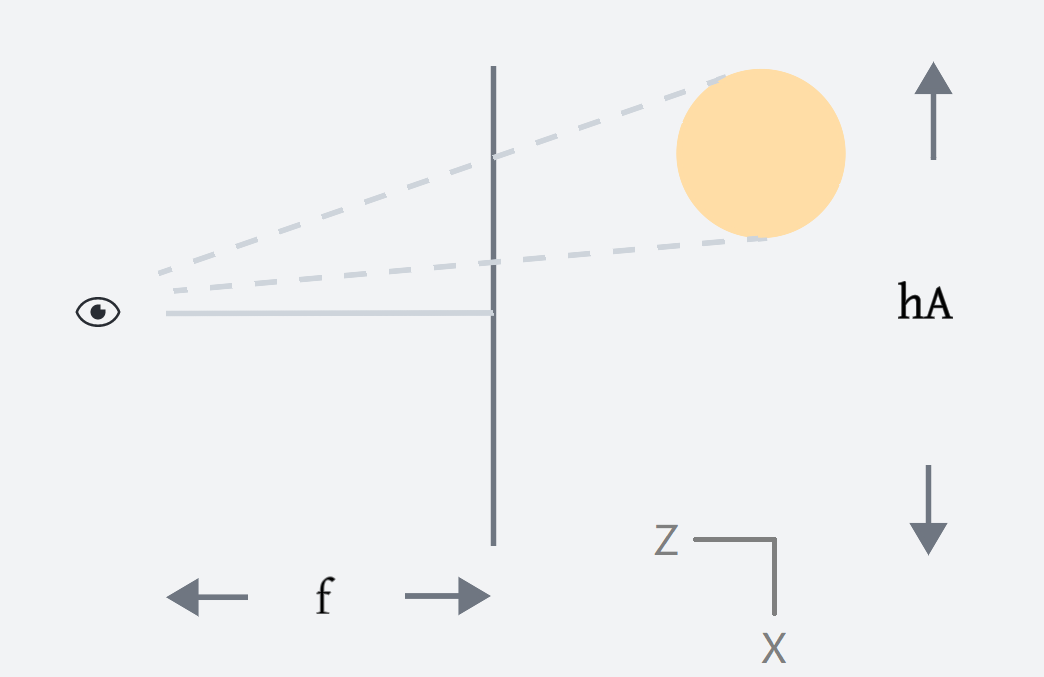
In the picture, f, which is the distance from the camera to the projection plane, is focal_length. hA is the distance from the left edge (upper end) to the right edge (lower end) and stands for horizontal_aperture.

near_clip and far_clip define two planes perpendicular to the line of vision between which you can see things.

Assumptions#

The following assumptions are made in frame of reference and conversion from/to other common representations.

If no transform operator is applied on the camera, the Y-axis points upwards and X-axis points to the right. The camera looks towards negative direction of the Z-axis.

There are many standards out there for the pinhole camera. To avoid confusion, we define a value called the $p i n h o l e R a t i o$ such that $p i n h o l e R a t i o = \frac{2 * f o c a l L e n g t h * a s p e c t R a t i o}{h o r i z o n t a l A p e r t u r e}$

If you are familiar with OpenGL/Direct3D, $f o v y$ is used more often.

p i n h o l e R a t i o = \frac{1}{\tan (f o v y / 2)}

If you are familiar with the intrinsic matrix or the Objectron standard, $f x, f y, c x, c y$ are used.

\begin{array}{r} f x = \frac{s c r e e n W i d t h \cdot p i n h o l e R a t i o}{2 \cdot a s p e c t R a t i o} \\ f y = \frac{s c r e e n H e i g h t \cdot p i n h o l e R a t i o}{2} \\ c x = s c r e e n W i d t h / 2 \\ c y = s c r e e n H e i g h t / 2 \end{array}

Here, $a s p e c t R a t i o = s c r e e n W i d t h / s c r e e n H e i g h t$ .